PENDIENTE DE UNA RECTA
Antes de referirnos a la orientación de una pendiente de la recta (si es positiva o negativa) hagamos una recapitulación:
Veamos un ejemplo.
Si tenemos
y = 3x − 4 esto es igual a,
3x − y − 4 = 0 (ecuación de la recta)
Ahora lo que sigue es sacar la pendiente, pero ¿Cómo se obtiene la pendiente si solo tenemos la fórmula?
Pues hay dos maneras de hacerlo: directa e indirecta:
Indirecta:
Obtenemos dos puntos (x e y) a partir de dos valores dados a x (por ejemplo, x = 1 y x = 2), y los ponemos en la ecuación de la recta:
3x − y − 4 = 0 si (x = 1)
3(1) − y − 4 = 0
3 − y − 4 = 0
y − 7 = 0
y = 7
P1 (1, 7) = (x1, y1)
3x − y − 4 = 0 si (x = 2)
3(2) − y − 4 = 0
6 − y − 4 = 0
y − 10 = 0
y = 10
P2 (2, 10) = (x2, y2)
Ahora sustituimos en la fórmula de la pendiente:
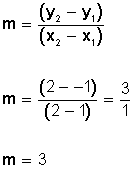
(esta es la pendiente)
Directa:
Basándonos en los valores de la recta podemos conseguir la pendiente:
3x − y − 4 = 0
Ax − By − C = 0
A = cantidad de x
B = cantidad de y
C = Número cualquiera
Ahora solo sustituimos en la fórmula de la pendiente
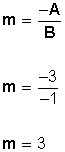
(esta es la pendiente)
Grado de inclinación
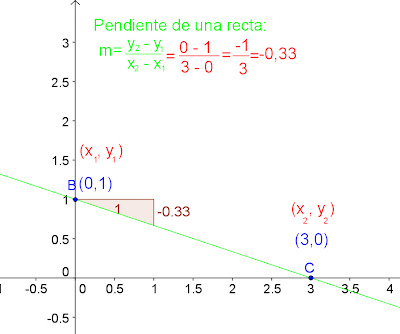
Dada una recta, gráficamente su pendiente nos da su grado de inclinación
Pendiente positiva
Cuando la recta es creciente (al aumentar los valores de x aumentan los de y), su pendiente es positiva, en la expresión analítica m > 0
Pendiente negativa
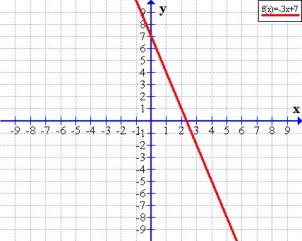
Cuando la recta es decreciente (al aumentar los valores de x disminuyen los de y), su pendiente es negativa, en la expresión analítica m < 0
Pendiente nula o cero
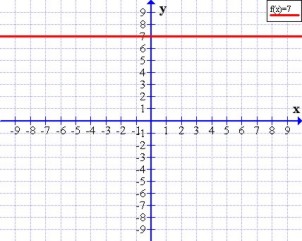
Cuando la recta es constante se dice que tiene pendiente nula, en la expresión analítica m = 0
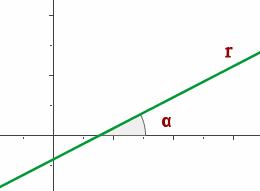
Visualmente, también podemos definir si la pendiente es positiva o negativa:
Si el ángulo que forma la recta con la parte positiva del eje OX es agudo, la pendiente es positiva y crece al crecer el ángulo.
Si el ángulo que forma la recta con la parte positiva del eje OX es obtuso, la pendiente es negativa y decrece al crecer el ángulo.
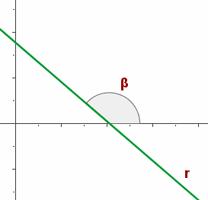
Con los ejemplos discutidos podemos observar la interpretación geométrica de la pendiente de una recta:
| Pendiente |
Tipo de recta
|
positiva
|
recta ascendente
|
negativa
|
recta descendente
|
cero
|
recta horizontal
|
no definida
|
recta vertical
|
La recta, o línea recta, en geometría, es el ente ideal que sólo posee una dimensión y contiene infinitos puntos, se puede representar como un vector; está compuesta de infinitos segmentos. El segmento es el fragmento mas corto de una linea que une dos puntos. La recta también se describe como la sucesión continua e indefinida de puntos en una sola dimensión, es decir, sin mostrar ni principio ni fin. También existe la recta numérica que es de las mismas características pero esta representando el orden de los numero.

UNA LINEA RECTA
Una recta queda determinada completamente si se conocen dos condiciones, por ejemplo, dos de sus puntos, un punto y su dirección (pendiente o coeficiente angular), etc.
La pendiente de una recta corresponde al cambio en Y dividido el cambio en X la cual corresponde a la ecuación:
Características de la Recta
La recta se prolonga al infinito en ambos sentidos.
La distancia más corta entre dos puntos está en una línea recta, en la geometría euclidiana.
La recta es un conjunto de puntos situados a lo largo de la intersección de dos planos.
Ecuaciones de la Recta
Tomados dos puntos de una recta, la pendiente m es siempre constante. Se calcula mediante la ecuación:
Ecuación General de la Recta
Ecuación de la Recta (vertical)
Ecuación de la Recta (horizontal)
Ecuación de la Recta (punto-pendiente)
Se puede obtener la ecuación de la recta a partir de la fórmula de la pendiente.
Esta forma de obtener la ecuación de una recta se suele utilizar cuando se conocen su pendiente y las coordenadas de uno de sus puntos, o cuando se conocen sólo los dos puntos, por lo que también se le llama ecuación de la recta conocidos dos puntos, y se le debe a Jean Baptiste Biot. La pendiente m es la tangente de la recta con el eje de abscisas X.
Ejemplo
Hallar la ecuación general de la recta que pasa por el punto A (4, -8) y que tiene una pendiente de 3/2 al sustituir los datos en la ecuación, resulta lo siguiente:
De esta forma hallamos la ecuación general de la recta la cual es de la forma:
Ecuación de la Recta (pendiente-intersección)
Si se conoce m (pendiente) , y el punto donde la recta corta al eje de ordenadas es (0, b), podemos deducir, partiendo de la ecuación punto pendiente de la recta,
Esta es la ecuación de la recta pendiente-intersección o pendiente intercepto.
Se utiliza cuando se conoce la pendiente y la ordenada al origen, que llamaremos b. También se puede utilizar esta ecuación para conocer la pendiente y la ordenada al origen a partir de una ecuación dada.
Solución para problemas en que la Recta pasa por un punto

Determinar las rectas del plano que pasan por el punto (x0,y0).
La ecuación de la recta ha de ser, como ya se sabe:
Y ha de pasar por el punto (x0,y0), luego tendrá que cumplirse:
Despejando b, tenemos esta ecuación:
Sustituyendo b en la ecuación general de la recta:
Ordenando términos:
Esta ecuación define un haz de rectas en el plano que pasa por el punto (x0,y0), el valor de m es la pendiente de cada una de las rectas que forman parte del haz, m puede tomar un valor real cualesquiera.
Distancia entre puntos
- Esta ecuación parte de tener dos puntos cualesquiera en el plano, llamándoles (x1, y1) y (x2, y2) la cual es una aplicación del teorema de Pitágoras siendo la distancia entre los puntos de cada uno de sus respectivos ejes los catetos, y la hipotenusa la distancia final.
- La distancia entre los puntos P1 y P2 denotada por d = P1P2, entre valor absoluto esta dada por:

Demostración:

Pendiente y ángulo de inclinación de una recta
El ángulo de inclinación de una recta es el ángulo que forma con el eje x. La medida del ángulo se toma en sentido contrario a las agujas del reloj.
La pendiente o tangente de un ángulo determina el ángulo de inclinación de la recta, es lo que se llama tangente inversa:
La pendiente (GE/AE) es igual a la tangente del ángulo:
m = tan h, o lo que es lo mismo 1/tan (o tangente elevado a -1) de la pendiente es igual al ángulo h.
arco tan (de la pendiente)=ángulo
Por ejemplo, el arco cuya tangente (segmento verde) es 0,75 es de 36,87º.
El ángulo se calcula aplicando tangente inversa a la pendiente, esto quiere decir que si tenemos por ejemplo que la pendiente de una recta vale una unidad, el arco cuya tangente vale la unidad es de 45°.
Si tenemos por ejemplo que la pendiente de una recta es -1, esto quiere decir que la recta tiene una inclinación hacia la izquierda y que forma con el eje x 135°.Como la tangente en este caso es negativa, y tiene por valor -1, el ángulo de la misma va a ser -45. Si tomo 180° y le resto 45°, obtengo el ángulo real que forma esta línea con el eje x, que es 135°.
Para determinar la distancia entre dos puntos cualesquiera, se resta uno del otro:
Por ejemplo la distancia del punto tres al punto uno, que es igual a 3 - 1, o bien es igual a 1 - 3, en ambos casos son dos unidades la diferencia, sin tener en cuenta el signo.
En el dibujo tenemos que si restamos 3 - 0 tenemos tres unidades en equis, mientras que si restamos 0 - 1, tenemos una unidad en y, con signo negativo, lo que nos informa que la recta tiene pendiente hacia arriba a la izquierda.
Cualesquiera que sean los puntos BC, las proyecciones de ambos sobre los ejes condenados están dados por las fórmulas: X=x2-x1, Y=y2-y1.
La pendiente de una recta queda definida por el cociente entre la diferencia de las coordenadas en y y las coordenadas en x.
La pendiente de esta recta del dibujo es 1,8, esto quiere decir que cuando sube 1,8 unidades en vertical y hacia la derecha avanza 1 unidad en horizontal. Esta relación de proporción la podemos expresar con un triángulo rectángulo que tiene cinco unidades como cateto horizontal y nueve unidades como cateto vertical.
La pendiente se expresa por la letra m y es el cociente entre el cateto vertical y el cateto horizontal del triángulo rectángulo cuya hipotenusa es la recta de la que se quiere calcular la pendiente.
En la fórmula Punto-pendiente (fórmula encuadrada en el rectángulo azul) tenemos que al sustituir un punto cualquiera de coordenadas x2 y2 y la pendiente de la recta (definida por la letra m) obtenemos la ecuación de la recta que pasa por estos dos puntos dada su pendiente. Debajo de la fórmula en el rectángulo azul, tenemos un ejemplo de la ecuación cuya pendiente es 9/5.
Si despejamos los términos y dejamos sola la variable y obtenemos la ecuación ordinaria, mientras que si la ecuación queda igualada a cero tenemos la ecuación general.
El ángulo que forma una recta con el eje X se llama ángulo de inclinación de la recta. Si la recta es paralela al eje X el ángulo de inclinación es cero. La tangente del ángulo de inclinación de la recta con el eje X es el coeficiente angular de la recta. En el ejemplo del dibujo tenemos que cuando sobre el eje horizontal se avanza tres unidades, sobre el eje vertical avanzamos una, esto quiere decir que la pendiente de la recta es un tercio o 0,33.
Una recta inclinada hacia la izquierda tiene pendiente negativa, ya que el incremento del eje y debajo del eje x determina sobre y una dimensión negativa. En ejemplo del dibujo tenemos que la pendiente de la recta es -1/2 o también -1/2 partido por 1. Cuando avanzamos hacia la izquierda una unidad por el eje X subimos una con dos unidades por el eje y.
Una recta de pendiente -2,5 y su ecuación: -5 x-2y =14. La pendiente de una recta en esta ecuación queda definida por la expresión: m=-A/B, donde la letra A corresponde al coeficiente al lado de la variable x y la letra B corresponde al coeficiente de la variable y. Por tanto la pendiente de la recta es m= 5/-2=-2,5
Ejemplos de pendientes de distintas rectas: 6, 4, 2, 0.5, -1, -4, infinita, -0,33
Ejemplos de ángulos de inclinación de distintas rectas: 80.54º, 75.96º, 63.43º, etc.
Ángulo entre dos rectas
El ángulo que forman dos rectas es igual al ángulo agudo determinado por los vectores directores de las rectas.

Dos rectas son perpendiculares si vectores directores son ortogonales.
Ejemplos
Hallar el ángulo que forman las rectas:
1. 

2. 


3. 


Ángulo entre dos planos
El ángulo formado por dos planos es igual al ángulo agudo determinado por los vectores normales de dichos planos.

Dos planos son perpendiculares si vectores normales son ortogonales.
Ejemplo
Hallar el ángulo que forman los planos:

Ángulo entre recta y plano
El ángulo que forman una recta, r, y un plano, π, es el ángulo formado por r con su proyección ortogonal sobre π, r'.

El ángulo que forman una recta y un plano es igual al complementario del ángulo agudo que forman el vector director de la recta y el vector normal del plano.


Si la recta r y el plano π son perpendiculares, el vector director de la rectay el vector normal del plano tienen la misma dirección y, por tanto, sus componentes son proporcionales.
Ejemplos
1. Determinar el ángulo que forman la recta  y el plano
y el plano  .
.

2. Hallar el ángulo que forman la recta  y el plano
y el plano  .
.


3. Obtener el ángulo formado por el plano y la recta siguientes:



| FORMAS DE LA ECUACIÓN DE LA LINEA RECTA |
| 4.4.1.Ecuación De La Recta Que Pasa Por El Origen | |
| Considere la recta l que pasa por el origen 0 y forma un ángulo de inclinación | |
Como los triángulos OP1P’1, OP2P’2 y OP3P’3 son semejantes; se tiene que: La ecuación (1) es la ecuación de la recta que pasa por el origen y tiene pendiente conocida m. |
| 4.4.2. Ecuación De La Recta Conocida Su Pendiente m Y Su Intercepto b Con El Eje y | |
| Considere una recta l de la que se conocen m (m = tan | |
fig. 4.7.
P’’(x, Y), Y Como P’’ (x, Y) está sobre l’, entonces Ahora, el cuadrilátero OBPP’’ es un paralelogramo. Luego, P’’P = OB = b. Y se tiene que: Y = P’P = P’P’’ + P’’P = Y + b = mx + b. Es decir, para todo (x, y) La ecuación y = mx + b es la ecuación de la recta en términos de su pendiente m y su intercepto b con el eje y. |
| 4 .4.3. Ecuación De La Recta Que Pasa Por Un Punto Y De Pendiente Conocida Considere la recta l que pasa por un punto dado P1(x1, y1) y cuya pendiente m también es conocida. . |
Al restar de la ecuación (2) la ecuación (1) se elimina el parámetro b que se desconoce y se obtiene:fig. 4.8
y – y1 = m(x – x1) (3)
La ecuación (3) es conocida como la forma: PUNTO-PENDIENTE de la ecuación de la recta.Nótese que la ecuación (3) también puede escribirse en la forma: y = mx + (y1 – mx1). Lo que indica que el intercepto b con el eje y viene dado por: b = y1 – mx1 |
Sea l la recta que pasa por los puntos P1(x1, y1) y P2(x2, y2) y llámese m1 su pendiente.
....
Esto es y2 – y1 =fig. 4.9. La ecuación (3) se conoce como la forma: DOS-PUNTOS de la ecuación de la recta. Observaciones i. Nótese que la ecuación (2) nos proporciona el valor de la pendiente m y la ecuación (3) también puede escribirse en la forma:  Lo que indica que el intercepto de la recta l con el eje y viene dado por: ecuación de la resta (3) también puede escribirse en forma de determinante, así:  = 0 = 0 |
4.4.5. Ecuación segmentaria de la linea recta
Considere la recta l de la cual conocemos los interceptos a y b con los ejes x e y respectivamente (fig. 4.10)
y = 0, resulta x = a (Intercepto con el eje x) x = 0, resulta x = b (Intercepto con el eje y) |
. Ecuación general de la linea recta
La ecución Ax + By +C = 0 donde A, B, C son números reales y A, B no son simultáneamente nulos, se conoce como la ECUACIÓN GENERAL de primer grado en las variables x e y.
| La ecuación explícita de la recta cuando se conocen dos puntos excluye las rectas paralelas al eje y, cuyas ecuaciones son de la forma x = constante, pero todas las rectas del plano, sin excepción, quedan incluidas en la ecuación Ax + By + C = 0 que se conoce como: laecuación general de la linea recta, como lo afirma el siguiente teorema: TEOREMA La ecuación general de primer grado Ax + By + C = 0 (1) , A, B, C Demostración i. Se puede Considerar varios casos: En este caso, la ecuación (1) se transforma en By + C = 0,0de dondeA = 0, B diferente de 0.
ii.
iii.
obeservacionesfig. 4.13. i. Es posible escribir la ecuación general de la linea recta en varias formas, de tal manera que solo involucre dos constantes. Es decir, si A, B y C son todos distintos de cero, podemos escribir la ecuación (1), en las siguientes formas equivalentes: En cada una de las ecuaciones (1A), (1B) y (1C) existe esencialmente solo dos constantes independientes, por ejemplo Esto indica que para determinar la ecuación de una recta en particular, necesitamos conocer dos condiciones, como por ejemplo, dos puntos, un punto y la pendiente, en concordancia con lo establecido en los numerales anteriores. iii. Cuando la ecuación de una recta esta expresada en la forma general Ax + By + C = 0, su pendiente ó coeficiente angular con respecto al eje x, m viene dado por viene dado por Los coeficientes A y B se denominan coeficientes directores de la recta. |